NLP-guidance

Latent Dirichlet Allocation (LDA)

TL; DR

Before we start

In common with some of the clustering algorithms below, for this method we need to define the number k of topics in our corpus.

What does LDA give us?

LDA is a probabilistic method. For each document the results give us a mix of topics that make up that document. To be precise, we get a probability distribution over the k topics for each document. Each word in the document is attributed to a particular topic with probability given by this distribution.

Topics themselves are defined as probability distributions over the vocabulary. So our results are two sets of probability distributions:

The following diagram shows how this might work for three topics and 16 words in the vocabulary. The results for a particular document are the first graph, showing the mix of topics within it. Each topic is itself a probability distribution over words in the vocabulary.

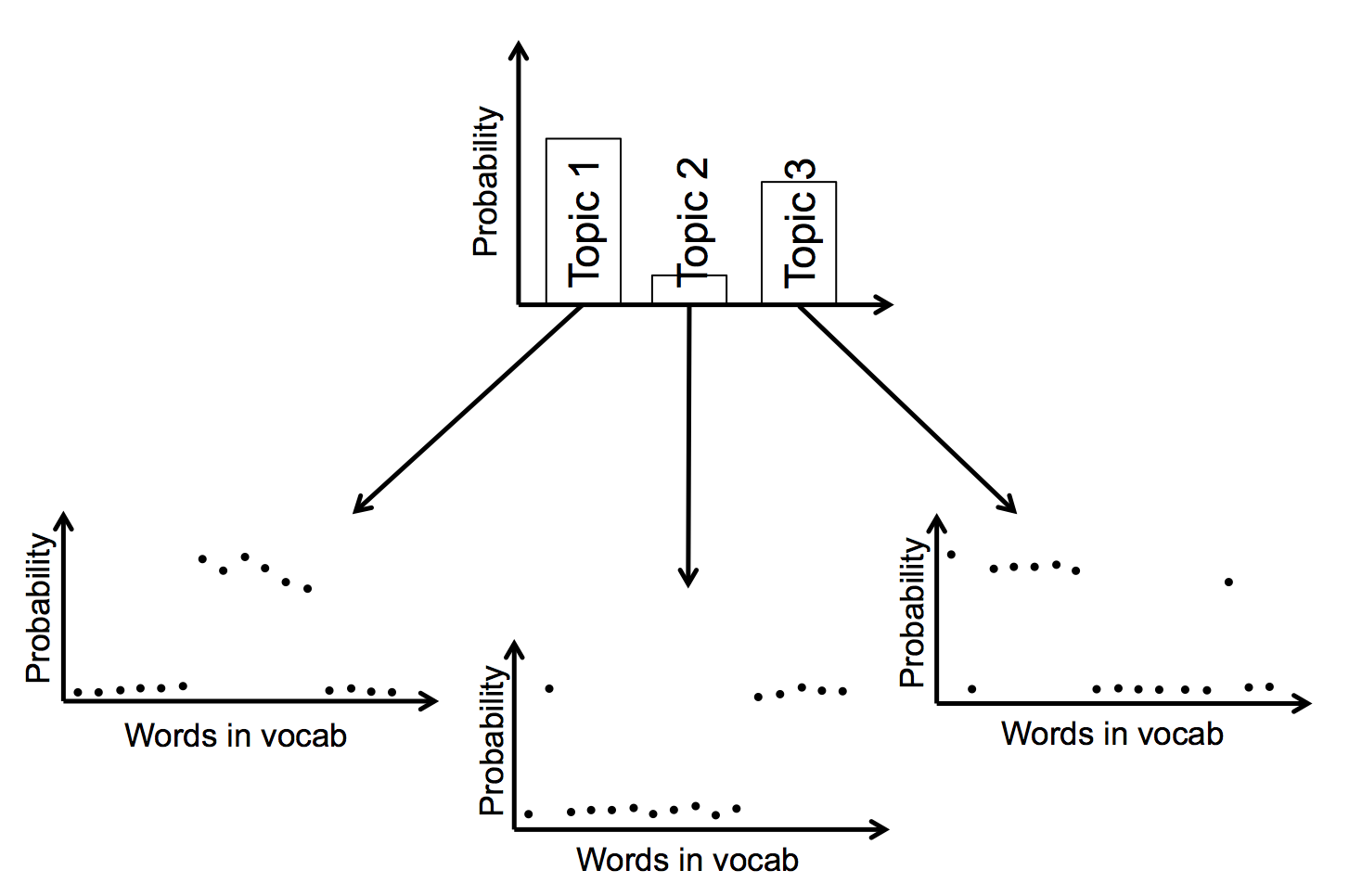
Example SVD from rank 2 to rank 1

The model is Bayesian, and doesn’t admit zero probabilities either for the topic distributions or for the word distributions. This means that in every document each topic has a non-zero probability, and in every topic each word in the vocabulary has a non-zero probability. However, these probabilities can be vanishingly small. Indeed, the model is set up so as to try and encourage most of the probabilities to be very close to zero: we want results that suggest each document is made up a small number of topics, and each topic is primarily composed of a small number of main words.

How do we get this?

There are a few different methods for generating an LDA, and I’m not going to go through them in any kind of detail here. But I think the reader should be aware of what the algorithms all do in general.

The results mentioned above give out, for k topics, with M documents, and a vocabulary of size N,

So the results provide k (M + N) values in total, or (once we take into account constraints) k (M + N) - k - M independent values (where all values must be from the interval (0, 1)). For any combination of these parameters we can estimate the likelihood of generating the actual documents that we see (e.g. the probability that we would get exactly these collections of words, given that our values for the distribution functions are correct). It is this likelihood function that the algorithms optimise, regardless of the specifics of their machinery.

Typically an algorithm will do something like: start in a random place on the (k (M + N) - k - M)-dimensional surface we are interested in, and do a guided random walk that ‘climbs the hill’ towards increasing this likelihood function; stop once further improvement is sufficiently unlikely that we think we are on a (local) optimum. To increase the chances of finding the global optimum, we run the process several times, starting from different random locations each time.

The point

The idea is that, armed with these results, you can look at the words that appear frequently within the topics and get a sense of what the topics are about. You can look at how the topics are distributed and see what the major themes are, both within documents and across the corpus. You can get tantalisingly close to being able to summarise a whole stack of texts automatically.

The problems

Unfortunately, we have not found it to quite work like that… We have tried using LDA on PQs and on consultation responses and are yet to get it to work in a satisfying way. Additionally, colleagues at Department for Transport had been using this approach for some work they were doing on consultations until we warned them about Problem 1 below, which they realised on inspection that they also suffered from.

We don’t claim that LDA doesn’t or can’t work in general, just that we haven’t yet managed to get it so that the results are usable. It may be that we just haven’t found the correct set of parameters for the algorithm, or it may be that in these cases the data isn’t appropriate for an LDA for reasons I don’t fully comprehend. Perhaps we need to do feature selection first. Regardless of why, here are the two main problems with LDA results as we’ve found them.

Problem 1: the results are not robust

While attempting this approach on consultations, we found that consultation responses that were identical were being assigned wildly different topical mixes. That is, we had two (or more) documents with identical wordings, and yet the LDA results were telling us that they were made up of completely different topics.

Since LDA results are probabilistic, we wouldn’t necessarily expect identically-worded documents to have the exact same topical distributions. But for the distributions to be completley different seems to me to render the results meaningless: if the topics purport to summarise the themes within the corpus, and if identical documents are being suggested to have completely different topics within them, then the credibility of the topics is irreparably damaged in my opinion.

It should be added that since writing this I have written a toy bit of code on LDA for this repo (found in the code folder) and have not managed to replicate this problem. So maybe it was just the package that we and DfT were using, or maybe it’s a problem that only crops up when you have a sufficiently large data set.

Update: using the topicmodels library in R, I haven’t been able to replicate this problem. So maybe it’s no longer a problem!

The next problem is still present, however.

Problem 2: the results are not explicable

This relates to problem 1, and in fact for a while this issue prevented us from discovering problem 1. All dimensionality reduction type approaches in natural language processing suffer from this to some extent, but the complexity of LDA makes it worse here in my opinion.

The results of an LDA give probability distributions for the topics over the vocabulary. In practice this means a list of words from the vocabulary, each with a probability associated with it. We can of course list the words in order of decreasing probability, and look at the top j words per topic for some j. We can look at all of the words above some threshold probability. We can look at words that occur with high probability within this topic when compared to their probability of occurrence across all topics (some very common words have high probability in all topics, while rare words might have low probability within this topic, but extremely low probability across the other topics). We can look at subtle and clever combinations of these values.

Regardless of what we do, we’re looking at a list of words that is somehow representative of this topic. But these words typically don’t fit together in an easily-comprehensible way. We don’t usually get a list like:

Topic x: banana, orange, grapefruit, peel, vitamin, five, watermelon

More usual is that, whichever method we use, we get some slightly odd mix of words and we have to strain a bit to say what this Topic is ‘about’ semantically.

An example is the LDA done on this guide by the example code. At the time of writing, this gives three topics. One of them clearly contains the mathematical terms, which is great. The other two have the following as most probable terms:

Topic 1: words, set, sam, written, ham, moj, https, good, word, back
Topic 3: vectors, documents, words, document, vector, lda, term, text, practice, terms

It’s hard for me to convincingly describe the semantic content of these topics with respect to this guide.

Now, of course, we could look at other measures to try to discover a telling list of terms associated with each topic. There are no shortage of options. We could consider the term-lift, which accounts for how prevalent a term is across all topics (e.g. “words” appears in Topics 1 and 3 above, and so is not a good way of distinguishing the meaning of these to topics). We could consider saliency, which accounts for “how informative the specific term is for determining the generating topic, versus a randomly-selected term” in an information-theoretic sense. We could go for relevance, which is an average of pure probability and the term-lift from above, weighted in some way of our choosing. We could no doubt pick various other options too.

Or we could start to worry that there are a lot of subtly-different measures here, and seemingly no obvious best choice.

My concern is that we are in danger of just trying lots of measures and picking the one that gives us what seems like the results we expect. I worry that we could do this and find spurious meaning even if we had completely random results, with no underlying relation to the words in our corpus (other than the same words and overall word frequencies).

I worry that we are just amplifying noise and projecting our own expectations on to it, rather than actually uncovering signal.

On the plus side, maybe we could try to instead get a good description of our Topic by looking at documents that have high content from this Topic and seeing what similarities they seem to have. I am a bit sceptical about this too, because a) these documents will also have other topical content, b) as we see from Problem 1, there is no reason to suspect that the topical content assigned to documents is robust, and c) if this procedure reliably worked, why would people keep coming up with new measures for term-to-topic relevance as seen above?

Conclusion

As you can tell, I am dubious and sceptical about a use case for LDA.

I hope that I am wrong, because the premise of topic modelling is a very seductive one. But if we can’t comprehensibly explain what our topics are about, and we can’t trust the assignment of topics to documents, it’s hard to see a use case.

If you are reading this and thinking “but I’ve got a perfect use case, where I found something novel and robust from a corpus using LDA”, and you can share it with me, then please get in touch at the email address below.

Back to contents

Written by Sam Tazzyman, DaSH, MoJ